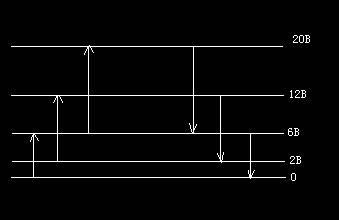
设散射物分子原来处于基电子态,振动能级如图所示。当受到入射光照射时,激发光与此分子的作用引起的极化可以看作为虚的吸收,表述为电子跃迁到虚态(Virtual state),虚能级上的电子立即跃迁到下能级而发光,即为散射光。设仍回到初始的电子态,则有如图所示的三种情况。因而散射光中既有与入射光频率相同的谱线,也有与入射光频率不同的谱线,前者称为瑞利线,后者称为喇曼线。在喇曼线中,又把频率小于入射光频率的谱线称为斯托克斯线,而把频率大于入射光频率的谱线称为反斯托克斯线。
附加频率值与振动能级有关的称作大拉曼位移,与同一振动能级内的转动能级有关的称作小拉曼位移:
大拉曼位移:v=v0+v',v= v0-v' (v'为振动能级带频率)
小拉曼位移:v~= v0~±(6+4J)B,J=0,1,2… (其中B为转动常数)
简单推导小拉曼位移:利用转动常数 B=h/4 πIc
转动能级Ej=J(J+1)h2/2I=J(J+1)hcB
能级的选择定则为:△J=±2
所以有E-E0=±(6+4J)hcB即v~=v0~±(6+4J)B,J=0,1,2…
谱线特征
拉曼散射光谱具有以下明显的特征:
a.拉曼散射谱线的波数虽然随入射光的波数而不同,但对同一样品,同一拉曼谱线的位移△v~与入射光的波长无关,只和样品的振动转动能级有关;
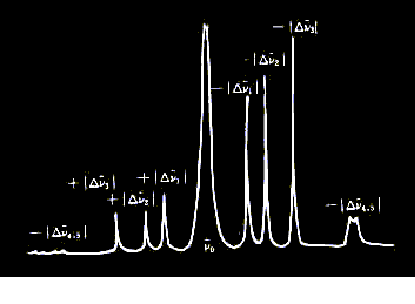
b. 在以波数为变量的拉曼光谱图上,斯托克斯线和反斯托克斯线对称地分布在瑞利散射线两侧, 这是由于在上述两种情况下分别相应于得到或失去了一个振动量子的能量。
c. 一般情况下,斯托克斯线比反斯托克斯线的强度大。这是由于Boltzmann分布,处于振动基态上的粒子数远大于处于振动激发态上的粒子数。
简单解释:按照波尔兹曼分布律,处于激发态 Ei的分子数Ni与处于正常态E0分子数N0之比是:Ni/N0=(gi/go) ×exp(-Ei-E0)/kT其中g为该状态下的简并度,对于振动态gi=g0=1,而Ei-E0>>kT所以,Ni<<N0 。
可以解释:温度升高,反斯托克斯线的强度迅速增大,斯托克斯线强度变化不大转动能级中,Ej=J(J+1)h2/2I所以,Ei-E0=h2/I<<kT 由于较低和较高的转动态都有显著的布居,所以小拉曼位移两组谱线(反斯托克斯线,斯托克斯线)强度差不多。
实验中光谱的分析
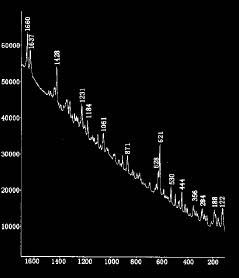
实验做出的谱图(见附图,以波长为单位)
标准的谱图(如下,以波数为单位)
通过CCl4的结构分析解释光谱:
分子为四面体结构,一个碳原子在中心,四个氯原子在四面体的四个顶点。当四面体绕其自身的一轴旋转一定角度,或记性反演(r—-r)、或旋转加反演之后,分子的几何构形不变的操作称为对称操作,其旋转轴成为对称轴。CCI4有13个对称轴,有案可查4个对称操作。我们知道,N个原子构成的分子有碍(3N—6)个内部振动自由度。因此CCl4分子可以有9个(3×5—6)自由度,或称为9个独立的简正振动。根据分子的对称性,这9种简正振动可归纳成下列四类:
第一类,只有一种振动方式,4个氯原子沿与C原子的联线方向作伸缩振动,记作v1,表示非简并振动。
第二类,有两种振动方式,相邻两对CI原子在与C原子联线方向上,或在该联线垂直方向上同时作反向运动,记作v2,表示二重简并振动。
第三类,有三种振动方式,4个CI与C原子作反向运动,记作v3,表示三重简并振动。
第四类,有三种振动方式,相邻的一对CI原子作伸张运动,另一对作压缩运动,记作v4,表示另一种三重简并振动。
上面所说的“简并”,是指在同一类振动中,虽然包含不同的振动方式但具有相同的能量,它们在拉曼光谱中对应同一条谱线。因此,CCl4分子振动拉曼光谱应有4个基本谱线,根据实验中测得各谱线的相对强度依次为v1>v2>v3>v4。苯的谱线也见附图,分析类似,这里不再赘述。
拉
拉曼光谱的应用
通过对拉曼光谱的分析可以知道物质的振动转动能级情况,从而可以鉴别物质,分析物质的性质.下面举几个例子:
天然鸡血石和仿造鸡血石的拉曼光谱有本质的区别,前者主要是地开石和辰砂的拉曼光谱,后者主要是有机物的拉曼光谱,利用拉曼光谱可以区别二者。
天然鸡血石的拉曼光谱:
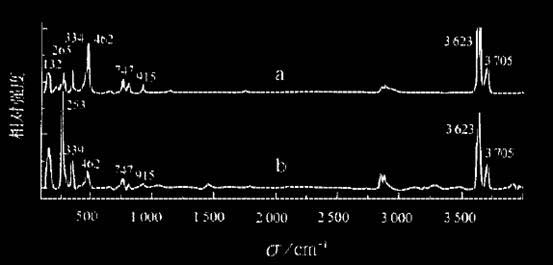
仿造鸡血石的拉曼光谱:
上两个图中,a是地(黑色),b是血(红色)
查阅资料,对不同物质的拉曼光谱进行比对,可以知道,天然鸡血石“地”的主要成分为地开石,天然鸡血石样品“血”既有辰砂又有地开石,实际上是辰砂与地开石的集合体。仿造鸡血石“地”的主要成分是聚苯乙烯-丙烯腈,“血”与一种名为PermanentBordo的红色有机染料的拉曼光谱基本吻合。
鉴别毒品:使用拉曼光谱法对毒品和某些白色粉末进行了分析,谱图如下